Here is another proof that √ 2 is irrational (Tom Apostol ; thx to The Universe of Discourse) :
 If √ 2 is rational, one can rescale the isosceles right triangle with hypothenuse √ 2 into a isosceles right triangle
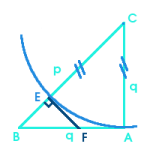
with integer sides. Let ABC be the smallest isosceles right triangle with integer sides q and p.
If √ 2 is rational, one can rescale the isosceles right triangle with hypothenuse √ 2 into a isosceles right triangle
with integer sides. Let ABC be the smallest isosceles right triangle with integer sides q and p.The circle centered at C of radius q intersects [BC] at E, where BE = p-q is integer.
The tangent to the circle at E intersects [AB] at F. BEF is right isoceles in E since EBF=BFE=45°. (FE) and (FA) are tangential to the same circle so FA equals FE, i.e. BE, and hence is integer, implying that BF = q-FA is integer.
BEF is a isosceles right triangle with integer sides, contradicting that ABC is the smallest one.
To be continued below...
Well... with x = √ 2 and y = √ 2 we have x^y = √ 2 ^ √ 2... Is this number rational ?
If it is the case we're done, else we try x = √ 2 ^ √ 2 and y = √ 2.
Hence x^y = 2 ! qed... (note : the Gelfond-Schneider tells us that the second case is the correct one)