D'abord, √ 2 est irrationnel... En effet si √ 2 = p/q avec pgcd (p,q)=1 alors p²=2q² donc p² est pair donc p aussi donc p² est multiple de 4 d'où q² est pair d'où q est pair également et donc pgcd (p,q)!=1... OK ?

Allez une autre preuve de l'irrationnalité de √ 2 (Tom Apostol ; merci à The Universe of Discourse) :
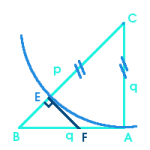
Si √ 2 est rationnel, on peut redimensionner le triangle rectangle isocèle d'hypothénuse √ 2 en un triangle rectangle isocèle ayant ses côtés entiers. Soit ABC le plus petit triangle rectangle isocèle de côtés q et p entiers.
Le cercle centré en C de rayon q coupe [BC] en E, avec BE = p-q entier.
La tangente au cercle en E coupe [AB] en F. BEF est rectangle isocèle en E puisque EBF=BFE=45°. (FE) et (FA) sont tangentes au même cercle donc FA vaut FE, i.e. BE, et est entier, ce qui entraîne que BF = q-FA est entier.
BEF est un triangle rectangle isocèle de côtés entiers, ce qui contredit la minimalité de ABC.
La suite plus bas...





































Bon... avec x = √ 2 et y = √ 2 on a x^y = √ 2 ^ √ 2... C'est rationnel ça ?
Si oui, c'est gagné... Sinon on pose x = √ 2 ^ √ 2 et y = √ 2.
On a alors x^y = 2 ! Voilà... (note : le théorème de Gelfond-Schneider nous dit que le second cas est le correct)