Note : je devais être d'humeur finie quand j'ai écrit ce texte il y a trois ans. Je ne sais pas aujourd'hui à quel point je suis d'accord avec lui. -SA (2001)

---

1. Introduction

Puisque la conscience est si peu connue, il semble souvent qu'on puisse affirmer n'importe quoi à son propos sans aucune peur que le contraire ne soit prouvé. Par exemple, quelqu'un pourrait prétendre que le véritable siège de la conscience est une noix de cajou invisible située dans le pancréas, et mettre au défi les scientifiques de trouver une meilleure explication. Ou bien on pourrait spéculer que la conscience émerge des lois de la gravité quantique, non calculables, encore indécouvertes, opérant au sein de structures cérébrales appelées microtubules, comme l'a fait Roger Penrose dans son livre de 1994 Shadows of the Mind [Pen94]. Cependant il y a un fait rarement discuté qui nous apporte quelque chose de tangible et d'important à propos de la conscience, et sa véracité est facile à établir. C'est que la conscience n'est pas infinie.

Aujourd'hui nous savons que le cerveau est un objet physique fini, contenant environ 100 millions de neurones et 100 milliards de synapses reliant ces derniers. Mais en disant que la conscience est finie, je parle de quelque chose de plus fort : il n'existe qu'un nombre fini de vies qui puissent être vécues ; et par conséquent, le libre-arbitre, s'il existe, se réduit à un certain niveau à la sélection d'un élément dans un ensemble fini. Le but de cet article est triple : montrer que cette proposition est vraie, discuter en quoi elle affecte la théorie de la conscience de Penrose, et enfin expliquer pourquoi nous n'avons pas à nous inquiéter de la finitude de nos esprits.

2. La finitude

Peut-être as-tu la sensation d'être capable de faire une infinité de choses avec ton ordinateur. Tu peux visiter des sites traitant des armes médiévales ou de l'inflammabilité des "Pop Tarts" ; tu peux jouer au démineur ou à Quake, ou faire danser le pointeur de la souris sur l'écran, ou écrire un programme, ou un article sur la conscience - sûrement cette variété de sujets n'a pas de fin ? Mais à regarder de plus près, ton ordinateur est un objet fini. S'il peut stocker N bits d'information en mémoire (où éventuellement N >> 500 millions) alors cette mémoire a au plus 2^N états possibles et à tout instant son état est une fonction déterministe de son état précédent et de l'entrée courante (ici 'entrée' se réferre non seulement au clavier, à la souris, aux micros, etc, mais aussi au disque dur, aux lecteurs CD et de disquettes, à l'horloge interne, aux autres périphériques et à l'environnement). En d'autres termes, ton ordinateur est ce qu'on appelle un automate à états finis, ou AEF (cf Hayes [Hay95]).

De plus, le temps, pour ton ordinateur, est divisé en unités discrètes, de telle façon que vu comme un AEF, il aurait seulement, disons, 200 millions d'opportunités par seconde de changer d'état. Ainsi clairement il existe une borne supérieure M sur le nombre de transitions d'états que ton ordinateur peut effectuer avant de mourir. Conservateurs, nous allons fixer M à un milliard de milliards de milliards de milliards de milliards (10⁴⁵), qui est bien plus de transitions que ton ordinateur pourrait faire entre maintenant et l'instant où l'univers s'effondrera dans un Big Crunch ou dégénérera en trou noir. Donc, élever le nombre d'états possibles à la puissance M nous donne une borne supérieure brute sur le nombre de choses que ton ordinateur pourrait faire. Ce nombre n'est pas infini, il est au plus 2^MN.

Voilà une conséquence déconcertante : si tu as des amis avec lesquels tu as interagi uniquement en ligne, alors l'historique complet de ces interactions peut être décrit par une de ces 2^MN possibilités. Dans ce sens, tu ne 'crées' pas tes conversations en ligne ; tu ne fais que choisir au sein d'un éventail de possibilités pré-existantes, large mais fini. La même chose peut être dite des conversations téléphoniques transitant par des relais numériques. Comme l'indique Richard Dawkins [Daw95, p. 14],

"Lors des longs débats avec ton amant(e) au téléphone, chaque nuance, chaque altération de la voix, chaque soupir passionné, le ton langoureux, tout cela est transporté le long du fil uniquement sous forme de nombres. Tu peux être ému(e) aux larmes par des nombres - à condition qu'ils soient codés et décodés suffisamment rapidement."

A cela j'ajouterais que les tons langoureux peuvent non seulement être codés par des nombres, mais en plus par des nombres de taille bornée - c'est-à-dire par un nombre fini d'entre eux.

Ces considérations s'appliquent aux conversations, mais également à n'importe quelle information stockable sur ton ordinateur. Les oeuvres complètes de Shakespeare téléchargées du projet Gutenberg, Mona Lisa sous forme d'image JPEG haute résolution, la 5^e symphonie de Beethoven encodée en fichier audio MP3, ne sont que des sélections de cet espace de 2^MN possibilités. Ce qui soulève une question intéressante : comment la 'créativité artistique' peut-elle exister si chaque oeuvre d'art n'est qu'une sélection parmi de multiples formes pré-existantes ? Cela ne serait certainement pas de la créativité si, présenté à un sac de bonbons, tu en choisissais un rouge. Je reviendrai à ce sujet en section 5.

Pour l'instant, voyons à quel point notre 'finitisation' de l'expérience humaine peut aller. Nous avons vu que seul un nombre fini de conversations télephoniques pouvaient être conduites via un relais numérique. Mais qu'en est-il des conversations via un relais analogique ? Ou des conversations face à face ? Des premiers baisers ? Des promenades à travers le parc un jour d'automne ? J'affirme qu'il n'y a qu'un nombre fini de possibilités pour chacune de ces choses, et en fait pour toute l'expérience humaine. Cela n'exige que le fait qu'un ordinateur pourrait, en principe, simuler l'expérience du monde d'un humain de telle façon qu'il serait impossible pour l'humain de déterminer la différence avec la réalité - en d'autres termes que la 'réalité virtuelle en immersion totale' soit théoriquement possible. Tout d'abord, notons l'existence d'une borne supérieure T sur la durée de vie d'un humain. Encore une fois, pour être conservateurs, fixons T égal à 10¹⁰⁰⁰ secondes (>> 10⁹⁹² ans). Deuxièmement, à chaque instant le cerveau humain ne peut accepter qu'un nombre fini A d'entrées possibles (i.e. de signaux aux cortex visuel, olfactif, et somatosensitif), et ne peut produire qu'un nombre fini B de sorties (i.e. de signaux du cortex moteur). Mais combien de tels 'instants' K y a-t-il en une seconde ? Les neurones ne transmettent des signaux qu'à un taux d'au plus un par milliseconde, donc du point de vue du cerveau, on a probablement K < 1000. Mais encore une fois, nous serons conservateurs, et supposerons que K = 10¹⁰⁰⁰. (En vérité, selon la théorie quantique, le temps lui-même ne peut plus être divisé au-dela de l'échelle de Planck 10^-43 s). Donc le total de vie humaines pouvant être vécues est au plus (AB)^KT. Cet argument ne dépend pas de comment la conscience fonctionne ; même s'il existe une âme immatérielle, il ne peut résulter qu'au plus (AB)^KT possibilités.

3. L'erreur de l'Infini Virtuel

Tu peux objecter que, bien qu'il n'y ait qu'un nombre fini de conversations téléphoniques pouvant avoir lieu, de tableaux pouvant être peints, de vies humaines pouvant être vécues, les nombres sont si astronomiques que ça ne ferait aucune différence s'ils étaient infinis. Cette objection illustre ce qui pourrait être appelé 'l'Erreur de l'Infini Virtuel' : la confusion entre les concepts distincts d'arbitrairement grand et d'infini. Que nous, humains, commettions régulièrement cette erreur, est compréhensible : la capacité de distinction entre, disons, huit chèvres et dix chèvres, est sans auncun doute un avantage intéressant, mais un homme préhistorique tentant de différencier 10¹⁰⁰⁰ et une infinité de chèvres ne serait qu'en train de perdre du précieux temps de chasse. Dans le cadre d'une remarque informelle sur le vaste espace ou la richesse de Bill Gates, nous comprendrions tous ce que 'virtuellement infini' voudrait dire. Mais sérieusement, l'Erreur de l'Infini Virtuel ne peut que créer de la confusion. Pour comprendre pourquoi, nous devons introduire la notion d'ensemble.

Les mathématiciens notent la cardinalité (ou la taille) de l'ensemble des entiers naturels par ce que nous entendons habituellement par 'infinité', symbolisée par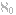 (prononcé aleph-zéro). 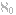n'est pas un nombre, et il n'y a aucun sens par lequel il pourrait être considéré comme 'la quantité la plus grande'. Dans les années 1880, Georg Cantor a montré que pour tout ensemble S (éventuellement infini), on peut former un plus grand ensemble en considérant l'ensemble de tous les sous-ensembles de S. L'étude des hauts ordres de l'infini a conduit aux incroyables théorèmes de Kurt Gödel (1938) et Paul Cohen (1963) selon lesquels l'existence d'un cardinal entre 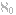et le cardinal des nombres réels [ndt : l'hypothèse du continu] est indécidable dans le cadre des axiomes usuels de la théorie des ensembles [Coh66], mais je digresse. Ce qui est important pour nous est qu'il est facile de montrer que 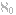est le plus petit ordre d'infinité - qu'il n'y a pas d'ensemble se tenant entre une cardinalité finie et infinie. Cela signifie qu'il y a une distinction nette entre les ensembles de taille N, où N peut être arbitrairement grand, et les ensembles infinis. Ces deux classes d'ensembles ont des propriétés très différentes : un ensemble infini peut ête placé en correspondance univoque (1 à 1) avec un de ses propres sous-ensembles (penser à l'ensemble des entiers et des entiers pairs [ndt : l'hôtel de Hilbert]), mais ce n'est pas le cas pour un ensemble fini, quelle que soit sa taille.

Les Grecs anciens étaient suspicieux vis-à-vis de l'infini à cause des 'paradoxes' liés à l'Erreur de l'Infini Virtuel, et en raison de cette suspicion l'humanité dût attendre deux millénaires qu'Isaac Newton et Gottfried Leibniz découvrent le calcul différentiel. Mais il est possible de se préserver de cette Erreur par cette simple règle : pour tout nombre N il y a une infinité d'entiers naturels plus grands que N. Cette règle implique que 2, 17, et le nombre d'expériences humaines possibles, sont tous à égale distance de l'infini.

4. Implications pour l'argument de Penrose

Quand Penrose déclare que la conscience émerge de processus non calculables du cerveau, il veut dire que ces processus ne peuvent être simulés par des machines de Turing. La machine de Turing est un modèle de calculabilité proposé par le mathématicien anglais Alan Turing en 1936. A première vue il semble bizarre ; il s'agit d'une tête de lecture/écriture se déplaçant en avant et en arrière, lisant et écrivant des symboles le long d'une bande magnétique infiniment longue divisée en carrés. Pourtant cette machine de Turing est capable de simuler tous les autres modèles de calculabilité ayant été proposés, amenant à la thèse de Church-Turing, stipulant que 'calculale par une machine de Turing' est ce que nous voulons dire par le terme 'calculable'. Mais existe-t-il des problèmes non calculables ? Turing a prouvé que la réponse était oui. Un exemple est le problème de l'arrêt. Etant données une machine de Turing M et une entrée I, decider si M va s'arrêter de fonctionner quand I est la configuration initiale des symboles sur la machine M. (S'il existait une machine de Turing qui pouvait résoudre ce problème, nous pourrions l'utiliser pour créer une autre machine de Turing H s'arrêtant de fonctionner si son programme d'entrée P tourne sans arrêt quand exécuté avec lui-même en tant qu'entrée. Puis nous pourrions exécuter H avec ell-même en tant qu'entrée, créant une contradiction.) Penrose maintient que simuler le cerveau humain fait partie de ces problèmes non calculables, et ceci est la base de ses spéculations sur la gravité quantiques et les microtubules. Avant que nous ne regardions pourquoi la finitude de nos esprits pose problème pour l'assertion de Penrose, examinons la raison originale de cette affirmation, basée sur le théorème d'incomplétude de Gödel.

Le théorème d'incomplétude affirme en gros qu'étant donné n'importe quel système formel consistant (i.e. ou aucun prédicat faux ne peut être prouvé) F permettant de raisonner sur les nombres, il existe une phrase de F, appelée G(F), vraie dans F mais simultanément improuvable au sein de F. Gödel a construit G(F) en commençant avec la phrase "Cette phrase est improuvable dans F", qui peut être facilement vue comme à la fois vraie et improuvable dans F lorsque F est consistant. Ensuite il montra comment exprimer cette phrase dans le langage de F, en codant les concepts de 'phrase' et de 'preuve' par des nombres [ndt : cf Gödel, Escher, Bach]. Le théorème de Gödel est une des pierres angulaires de la logique mathématique, mais Penrose affirme qu'il est également pertinent pour la conscience. Son raisonnement est que, alors qu'un ordinateur fonctionnant à l'intérieur du système formel fixe F ne peut pas prouver G(F), un humain peut voir sa véracité, et doit par conséquent posséder des capacités mentales au-delà de ces ordinateurs.

Cet argument n'est pas nouveau (il remonte au moins à John Lucas en 1961) ; les logiciens et les informaticiens ont depuis indiqué une faille majeure le concernant. C'est que les mathématiciens humains n'utilisent pas de systèmes formels consistant tels que F, ils ne se basent que sur l'intuition, et font fréquemment des erreurs. Si nous laissons à un ordinateur cette même liberté d'erreurs, il n'a pas besoin d'opérer strictement au sein de F, et il n'a y rien de paradoxal pour lui à 'voir' la véracité de G(F). Même sans cette considération, que le fait qu'un ordinateur fonctionne algorithmiquement n'implique pas qu'il doive ou devrait utiliser un système formel : si nous le programmons pour qu'il affiche '1+1=3' alors il s'accomplira. Penrose est conscient de cette faille, et il essaye longuement dans Shadows of the Mind de la réparer. Par exemple, il souligne que même si des mathématiciens font individuellement des erreurs, la communauté mathématique intégrale ne contredit jamais 'en principe' une affirmation mathématique ayant été établie comme vraie - mais évidemment elle le fait souvent en pratique ! Il déclare également que nous pouvons distinguer entre les erreurs 'corrigibles' des mathématiciens humains et leurs conclusions 'inattaquables', mais n'explicite jamais comment réaliser cela (cf McDermott [McD95]).

Mais réfuter l'argument de Penrose est similaire à la réfutation d'une méthode de quadrature du cercle ; bien que trouver la faille spécifique peut se révéler instructif, nous pouvons juger même avant de regarder les arguments qu'il doit y avoir une faille quelque part. Cela est possible parce que, comme nous l'avons vu, un esprit humain n'acepte qu'un nombre borné de bits d'entrée. Donc nous n'avons pas besoin de la pleine puissance d'une machine de Turing pour simuler un esprit : un automate à états finis (comme dans la section 2) suffira. Cela rend l'idée selon laquelle l'esprit a des capacités non calculables problématique. Avant de considérer la réponse de Penrose à cette objection, voyons sa taxonomie de vues sur l'état conscient [Pen94, p. 12] :

1. Toute pensée est calcul ; en particulier les sentiments d'état conscient sont produits purement par la conduite de calculs appropriés.
2. L'état conscient est une caractéristique de l'action physique du cerveau ; et alors que toute action physique peut être simulée algorithmiquement, la simulation algorithmique ne peut pas, par elle-même, produire la conscience.
3. Une action physique appropriée du cervau produit la conscience, mais cette action physique ne peut pas être simulée proprement par un ordinateur.
4. La conscience ne peut être expliquée par des termes physiques, calculables, ni aucun autre terme scientifique.

Les visions A et B sont, je pense, celles compatibles avec la certitude que la conscience est finie. Penrose affirme, sans surprise, que "la vision C est celle que je pense être la plus proche de la vérité" [Pen94, p. 15]. (Il dit au début qu'il se focalise sur des explications au sujet de la conscience essayant au moins d'être scientifiques, éliminant d'office la vision D.) Penrose atteint le point le plus proche de la question de la finitude de la conscience dans sa 'Q7' (une des vingt objections qu'il soulève contre sa propre théorie, ainsi que ses réponses). Bien que la 'Q8' traite aussi du fait que les ordinateurs et les cerveaux soient finis, elle fait appel à certains aspects des mathématiques ne nous concernant pas ici. Donc, examinons la Q7 [Pen94, p. 82-83] :

Le total de la production de tous les mathématiciens ayant vécu et de la production de tous les mathématiciens des (disons) mille prochaines années est fini et pourrait être emmagasiné dans les banques de mémoire d'un ordinateur adéquat. Clairement cet ordinateur particulier ne pourrait-il pas, par conséquent, simuler cette production et donc se comporter, vu de l'extérieur, de la même façon qu'un mathématicien humain - bien que l'argument de Gödel semble nous dire le contraire ?

Question à laquelle Penrose répond partiellement :

... On pourrait tout aussi bien envisager des ordinateurs ne contenant rien d'autre que des 'théorèmes' mathématiques complètement faux, ou des listes de mélanges de vérités et de faussetés. Comment pouvons-nous dire à quel ordinateur faire confiance ? Ce que j'essaye de mettre en valeur ici n'est pas qu'une simulation de la production consciente humaine (ici les mathématiques) est impossible, puisque par chance un ordinateur pourrait la reproduire, même sans aucune forme de quelconque compréhension. Mais la probabilité que cela arrive est absurdement faible, et les problèmes évoqués ici, à savoir comment décider quelles sont les affirmations mathématiques correctes et lesquelles sont fausses, ne sont même pas touchées par la Q7 [mise en italique : Penrose].

Cela résonne comme la vision B, contredisant directement la croyance revendiquée de Penrose de la vision C. Penrose peut répondre en mettant en évidence le mot 'proprement' dans la vue C, et en soulignant que simuler un esprit en énumérant simplement chacune de ses contingences, avec les réponses choisies, ne constitue pas une simulation 'propre'. Mais dans ce cas, pourquoi fait-il la distinction entre vues B et C ? (Penrose rend sa position assez floue dans un dialogue fantaisiste [Pen94, p. 179-190] entre un humain et un robot. Le robot devient fou quand l'humain le met au défi de prouver G(F), mais le fait que le robot puisse tenir une conversation articulée semble indiquer l'adhésion de Penrose à la vue A ou B.) Penrose n'a peut-être pas suffisamment considéré l'impact de la finitude de nos esprits sur sa théorie.

5. Pourquoi la finitude n'est pas si horrible

Nous avons vu que, indépendamment du fait que la conscience émerge de la complexité du cerveau, d'une âme incorporelle, ou de la gravité quantique et des microtubules, être conscient signifie, en fin de compte, sélectionner un élément dans un ensemble fini. Cela rend-il la conscience triviale ? Etant donnée l'insistance des mathématiques du 19^e siècle sur les relations de continuité et les ensembles infinis, un mathématicien de cette époque aurait répondu que oui. Mais depuis, il est apparu de plus en plus clair que la finitude n'impliquait pas la trivialité. L'informaticien Donald Knuth [Knu76] a écrit :

"Depuis les temps de la philosophie grecque, les savants se sont émeveillés de leur capacité à comprendre l'infini, et dans certains cercles il est devenu traditionnel de voir les choses finies comme essentiellement triviales, trop limitées pour être d'un quelconque intérêt. Il est difficile de démystifier une telle notion, car il n'y a ancun standard reconnu pour démontrer que quelque chose est intéressant, surtout quand ce quelque chose est comparé avec quelque chose de transcendant. Cependant je crois que ce climat de pensée évolue depuis que les processus finis se sont révélés être de si fascinants objets d'étude."

Alors comment les objets finis, encore relégués à l'insignifiant il y a moins d'un siècle, sont-ils parvenus à trouver une place correcte dans l'espace des mathématiques ? Une explication partielle peut provenir du travail de Paul Erdös, un des géants des mathématiques du 20^e siècle, qui à travers plus de 1500 publications a aidé à apporter de la repectabilité à l'étude des graphes et autres objets combinatoires finis. Le domaine des groupes finis a également peut-être joué un rôle. Ainsi, un groupe appelé "le Monstre" ne possède que 8 * 10⁵³ éléments et donc pourrait être complètement décrit par une table finie, mais en raison de ses connections à des domaines tels que les fonctions modulaires ou la théorie des cordes, ce groupe a occupé l'attention de la scène mathématiques durant de nombreuses années.

La plus grande motivation, cependant, a été l'ordinateur, qui a enclenché la création de nouvelles branches des mathématiques finies. Une de ces branches, appelée théorie de la complexité, traite de combien la durée et de l'espace mémoire requis pour résoudre un problème grandissent avec la taille de celui-ci. Par exemple, dans le problème de la Clique Maximum, on nous donne une liste de N personnes, ainsi qu'une liste des amitiés parmi ces N personnes, et il s'agit de trouver le plus grand groupe où chacun est ami de tous les autres. Nous pouvons résoudre n'importe quelle instance du problème de la Clique Maximum en examinant un nombre fini de groupes de gens (il y a 2^N possibilités), et donc le problème a l'air trivial. Mais 2^N croît tellement rapidement que, disons, quand N>>500, résoudre le problème aujourd'hui avec tous les ordinateurs existant acuellement demanderait plus de temps que l'âge de l'univers. Le problème de la Clique Maximum est appelé problème NP-complet (pour Nondeterministic Polynomial) et énormément de problèmes similaires sont infectés par cette même croissance exponentielle. Il est connu que s'il existe un algorithme efficace pour un problème NP-complet, il en existe pour tous les problèmes NP-complets - où 'efficace' est défini comme requérant une durée bornée par une fonction polynômiale de la taille N de l'entrée (genre N³). Ayant cherché en vain un tel algorithme efficace pendant des décennies, les théoriciens de la complexité supposent aujourd'hui qu'aucun de ces algorithmes n'existe, et cela s'appelle la conjecture P!=NP. Prouver (où prouver la fausseté de) P!=NP est aujourd'hui un des grands problèmes des mathématiques modernes, avec des implications dans des domaines tels que l'ingénierie, la recherche opérationnelle, la cryptographie, et même la nature de la créativité.

Cette dernière revendication peut paraître surprenante, surtout étant donnée la vision de Penrose selon laquelle "les questions soulevées par la théorie de la complexité ne sont pas exactement des questions centrales du point de vue des phénomènes mentaux" [Pen89, p. 145]. Alors, élaborons. Souvenez-vous que dans la deuxième partie, nous nous sommes demandés comment une oeuvre d'art peut être 'créative' si elle consistait simplement en une sélection parmi beaucoup de possibilités pré-existantes. La réponse, je crois, la plus populaire, serait que si un ensemble de possibilités est si énorme que deux personnes n'ont pas la moindre chance de choisir la même chose, le choix d'une des options peut être créatif en soi. Donc choisir un bonbon dans un sac contenant huit parfums différents ne serait pas créatif, mais choisir parmi 10¹⁰⁰⁰ parfums pourrait l'être. Souvent nous sommes confrontés à bien plus de 10¹⁰⁰⁰ choix quand nous écrivons un poème, composons une chanson, ou dessinons un portrait, parce que le nombre de choix croît exponentiellement avec le nombre de caractères, notes, ou pixels. Mais avoir un nombre exponentiel de choix ne garantit pas en soi que la créativité soit possible. Nous devons également savoir qu'étant donné un choix quelconque, l'évaluation de la 'beauté' de ce choix n'est pas traitable informatiquement - cela exigerait, disons, de simuler un cerveau humain entier pour calculer sa réaction à ce choix. Car s'il existait un algorithme efficace (polynômial) évaluant la beauté artistique, et si les théoriciens de la complexité découvraient un jour que P=NP, alors l'art serait rendu trivial ! Nous pourrions avoir des logiciels écrivant des poèmes 'optimaux', composant des chansons 'optimales', peignant des portraits 'optimaux' et les artistes de ces domaines seraient chômeurs. Comme il nous est difficile d'accepter que notre notion de créativité dépende de solutions de problèmes mathématiques non résolus, nous devons au moins exiger qu'évaluer une oeuvre d'art de taille N requière une durée exponentielle en N, voire exiger que le problème soit indécidable. (Les humains, bien sûr, ne peuvent pas effectuer de jugement esthétique 'heuristique' plus efficacement que cela.) Donc, bien que l'art n'implique qu'une sélection parmi un nombre fini de choix, la théorie de la complexité nous aide à comprendre que le choix peut être non-trivial en pratique.

Que nos esprits soient finis nous aide à faire la lumière sur certain arguments philosophiques comme celui de Penrose. Mais comme nous l'avons vu cela ne trivialise pas la conscience, ni ne diminue le rôle de la créativité. Donc cela ne me dérange pas que ma vie entière puisse être modélisée par le choix d'un élément dans un ensemble fini, et j'espère que cela ne te dérange pas non plus que la tienne puisse l'être également. La finitude de nos esprits peut même être source d'optimisme, car elle rend notre capacité à contempler l'infini encore plus étonnante.

Références

[Coh66] Cohen, Paul. Set Theory and The Continuum Hypothesis. Benjamin Books, 1966.

[Daw95] Dawkins, Richard. River Out of Eden. Basic Books, 1995.

[Hay95] Hayes, Brian. "Debugging Myself," American Scientist, September-October 1995.

[Knu76] Knuth, Donald. "Mathematics and Computer Science : Coping With Finiteness," in Selected Papers on Computer Science, CSLI Publications and Cambridge University Press, 1996. Originally published in Science, Volume 194, December 17, 1976.

[McD95] McDermott, Drew. "[STAR] Penrose is wrong," Psyche, September 22, 1995.

[Pen94] Penrose, Roger. Shadows of the Mind. Oxford University Press, 1996 (first printing 1994).

[Pen89] Penrose, Roger. The Emperor's New Mind. Penguin, 1991 (first printing 1989).